At the beginning of May, we shared the pentagon problem with the PKS community: can you discover or create an irregular pentagon that will tile the plane with no gaps or overlaps? Many students and parents rose to the challenge, and it has been so much fun having conversations about the various solutions and how they found them.
Mia from 4th grade was one of the first to stop by the math station, soon after the assembly. She shared her “House Pentagon,” which she said she came up with while she was thinking about the problem during assembly. A few minutes later, she came back to add the “Tooth Pentagon.”
Sage, a third grade student, brought in his “Flag Pentagon.” He explained that he had noticed the shape and a tiling pattern in his Legos. Do you notice that Sage’s Flag and Mia’s House are very similar?
Both feature two right angles. Sage could not remember exactly how the pentagons fit together, but the formation he saw was certainly different than the way in which Mia tiled her similar pentagon. I wonder if the Lego tiling may have looked like the example below. In any case, we can clearly see that this particular pentagon family could have many members (we could hypothetically extend the parallel sides infinitely, or alter the distance between them).
In fact, Caden from 2nd grade brought in another offering from this same pentagon family. We can see that his “Arrowgon” still has the pair of right angles and parallel sides, but the parallel sides are longer and the side perpendicular to the pair of parallel sides are much longer. Caden explained to me that he had discovered his pentagon while playing with Magna Tiles. “I put together the triangles and the squares,” Caden explained, “and then I noticed how they fit together, and I thought about your question about pentagons.”
So we can see that there is at least one family of pentagons with many members. What about Mia’s Tooth Pentagon? How does that one fit into this picture? Is it related to the Arrow, the House, and the Flag? What do you think?
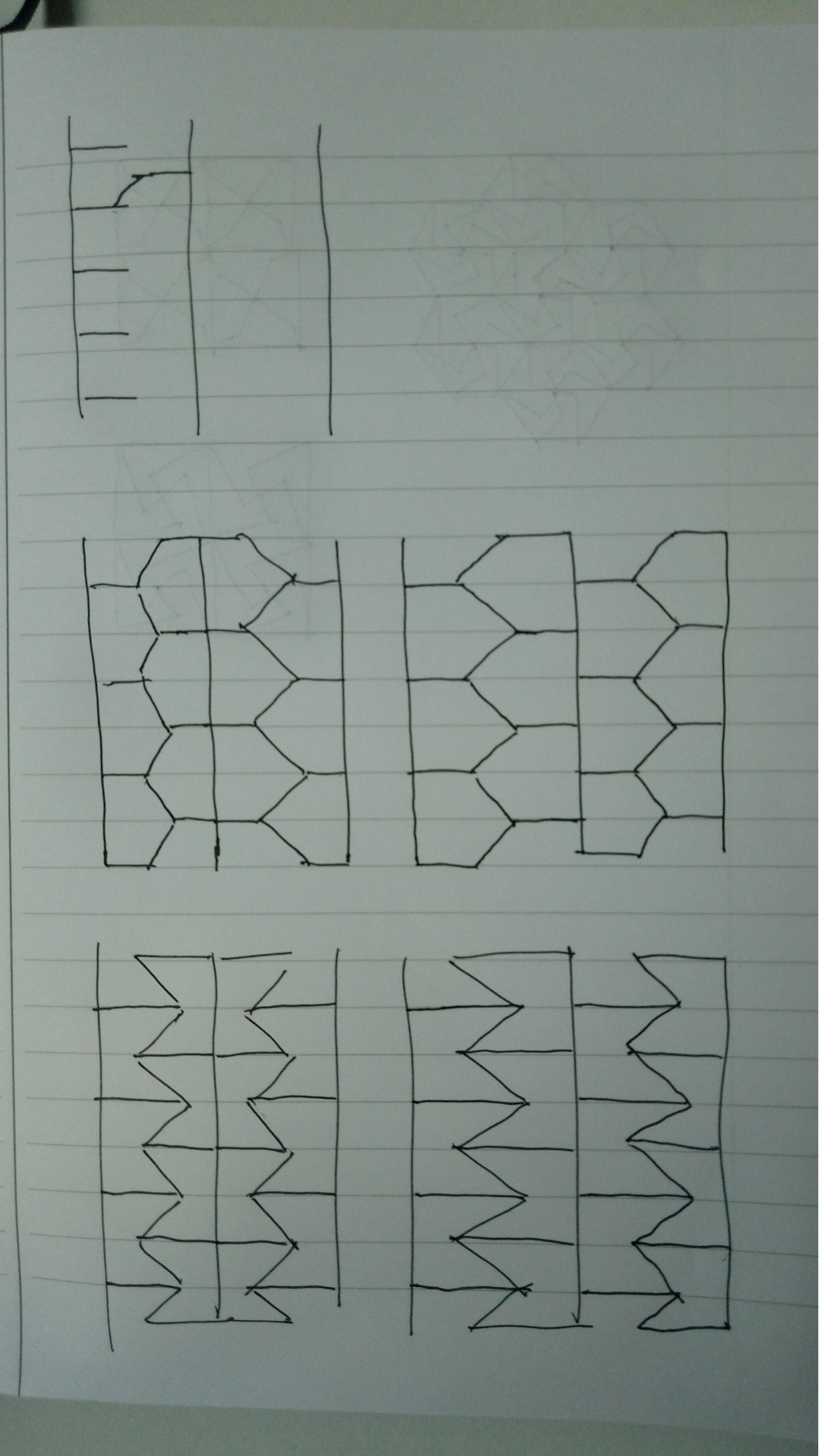
One of our first graders, Ryan, and his family, experimented with doodling and breaking up various shapes, and discovered both the Arrow/House/Flag and the Tooth by drawing long strips and dividing them into shapes, as you can see on the right. They took their investigation further by sketching other shapes that they knew tiled (like squares and hexagons) and splitting those to create some new offerings to the pentagon family.
Outside of the artistic submissions, I also had some interesting conversations with students who were thinking about tiling and pentagons after the assembly. Third grader Karina brought up the question of angles. She had noticed that the angles of some of the shapes just didn’t fit together (as with the regular pentagons). I asked her to think about what angles would need to be able to do to fit together like a puzzle. She wasn’t sure how many degrees were in a circle, but she did know what 90° looked like. By reflecting that familiar area, Karina figured out that a straight line would be 180° , so a circle would have 360° - therefore, for a shape to tile, it needs to have angles that can add up to 360°. So we figured out the problem with the regular pentagon - each interior angle measures 108°, which can’t possibly add up to 360°!
The story of the tiling pentagon is a fascinating one that brings together mathematics, history, and technology. I was inspired by an excellent talk I went to at the NCTM (National Council for the Teaching of Mathematics) Conference back in April. What I love about this story is that it shows how math is a living entity. Mathematicians and math lovers have been playing with tiling pentagons for more than a century, and the answer that we have now (there are exactly 15 convex pentagons that tile the plane) is a collaboration that took place over decades and involved trained mathematicians, amateurs who were interested in math, and ultimately, a computer algorithm. One of the major contributors was Marjorie Rice, who had no mathematical training, but approached the problem systematically and artistically to discover four new tiling pentagons (two are featured below, with art she developed to accompany the patterns).
Until very recently, though, we couldn’t be sure that there weren’t any still to be discovered pentagons. But Michaël Rao in 2017 developed a computer-assisted proof showing that there were exactly 15 families of tiling pentagons.
There is so much more to discuss and explore with tiling ! If you are interested, I encourage you to read Patrick Honner’s (the presenter who inspired me at NCTM) article and discuss some of these ideas with your children. Try printing out and playing with some of the pentagons and exploring the different ways in which they might tessellate, or tile. Some of them will fit together easily, while others might take some work to figure out. What other questions do you and your family have about shapes, angles, and tessellations? Don’t hesitate to send me a note if you discover something, or come up with an interesting question!